字典学习(dictionary learning)
什么是字典学习
字典学习的目标,提取事物最本质的特征(类似于字典当中的字或词语),它对我们对物体得到的信息降维,减少了无关紧要信息对定义这个物体的干扰。
理论依据
稀疏模型
$x=D\cdot \alpha$,
x是输入图像(维度$d_{i}$)
D字典模型 ($d_{2}K$)
$\alpha$ 稀疏矩阵 (K)
$min\Vert \alpha\Vert$
$$
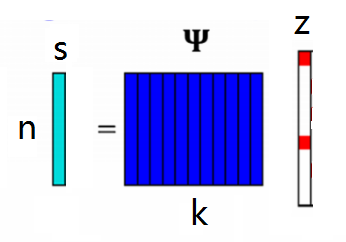
s=\psi z,(\psi \in \mathfrak{R}^{n\times k},z\in \mathfrak{R}^{k\times1},s\in\mathfrak{R}^{n\times 1})
$$
离散余弦变换和离散小波变换
利用信号经过这两种变换后都会有稀疏性的特性,把这两种变换变成矩阵形式,让信号直接投影到具有稀疏性的空间上。
好处
- 不需要特别针对信号做不同$\psi $的选择,对于绝大部分信号可以直接使用。
- 并不需要前处理,可以直接使用。
坏处
- 限制了原信号的维度,必须满足$n=2^x$,x为任意正整数。
- 因为通用所有信号,故经过压缩感知还原算法后还原的信号质量较差。
字典学习
把$\psi$当作一本要学习的字典,不断的利用该信号和还原算法后的结果做字典的更新,直到找到一个$\psi$ 能够把信号投影到稀疏性空间上。
字典学习的流程:
1.设置字典学习iter
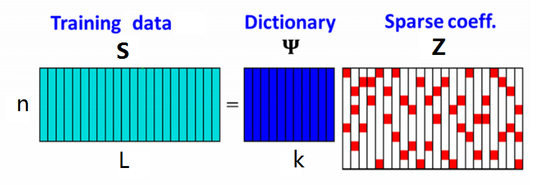
2.收集一定量的数据s,组成$S=[s_1,s_2\dots,s_L]$
3.固定$\psi $ 利用还原算法找出每一笔数据z 组成$Z=[z_1,z_2\dots ,z_L]$
$$
\min\limits_{c}\Vert S-\psi Z\Vert_F^2 s.t.\Vert Z_i\Vert_0 <K_{th} \forall i
$$
4.固定Z,利用3的Z来更新字典
Z固定时,定义误差$e_i=s_i-\psi z_i$组成$E=[e_1,e_2,\dots,e_L]$
整体的均方误差
$$
|\mathbf{E}|{F}^{2}=|[\mathrm{e}{1}, \mathrm{e}{2}, \ldots, \mathrm{e}{\mathrm{L}}]|{F}^{2}=|\mathbf{S}-\psi \mathbf{Z}|{F}^{2}
$$
固定Z使得E最小$(S-\psi Z)Z^T=0$ => $\psi =SZ^T(ZZ^T)^{-1}$
好处
- 因为针对该种类信号做学习,故还原后的质量较好。
- 对原信号的维度并没有任何限制。
坏处
- 需要事前收集该种类的信号做学习,不能未学习直接使用。
- 因为针对该种类信号做学习,故直接使用在不同种类信号效果较差/不适用。
[2018]Deep Convolutional AutoEncoder-based Lossy Image Compression
CAE convolutional autoencoder
PCA(principal components analysis)