Survey:空间曲率问题
空间曲率问题
空间曲率问题是一个微分几何问题。
三角网格离散曲率估计和Taubin方法改进.pdf 这篇文章对于这块内容解释得非常仔细,总结了包括了基本知识、连续性推导公式求法再到离散化。
基本知识
在二维情况下,曲线$y=f(x)$ 其曲率为
$\kappa ={\frac {|f’’(x)|}{(1+f’^{2}(x))^{\frac{3}{2}}}}$
对于一个以参数化形式给出的空间曲线其曲率为$c(t)=(x(t),y(t),z(t))$
平均曲率:$(k_{1} +k_{2})/2$
主曲率 :$k_{max}$ ,$k_{min}$
高斯曲率:$k_{max} *k_{min}$
平均曲率是一个“外在的”弯曲测量标准,局部地描述了一个曲面嵌入周围空间(比如二维曲面嵌入三维欧几里得空间)的曲率。
参数曲面可以表示成:p(u , v)= p(x(u,v), y(u,v),z(u,v)) (u,v)∈[ 0 , 1 ] ×[ 0 , 1 ]
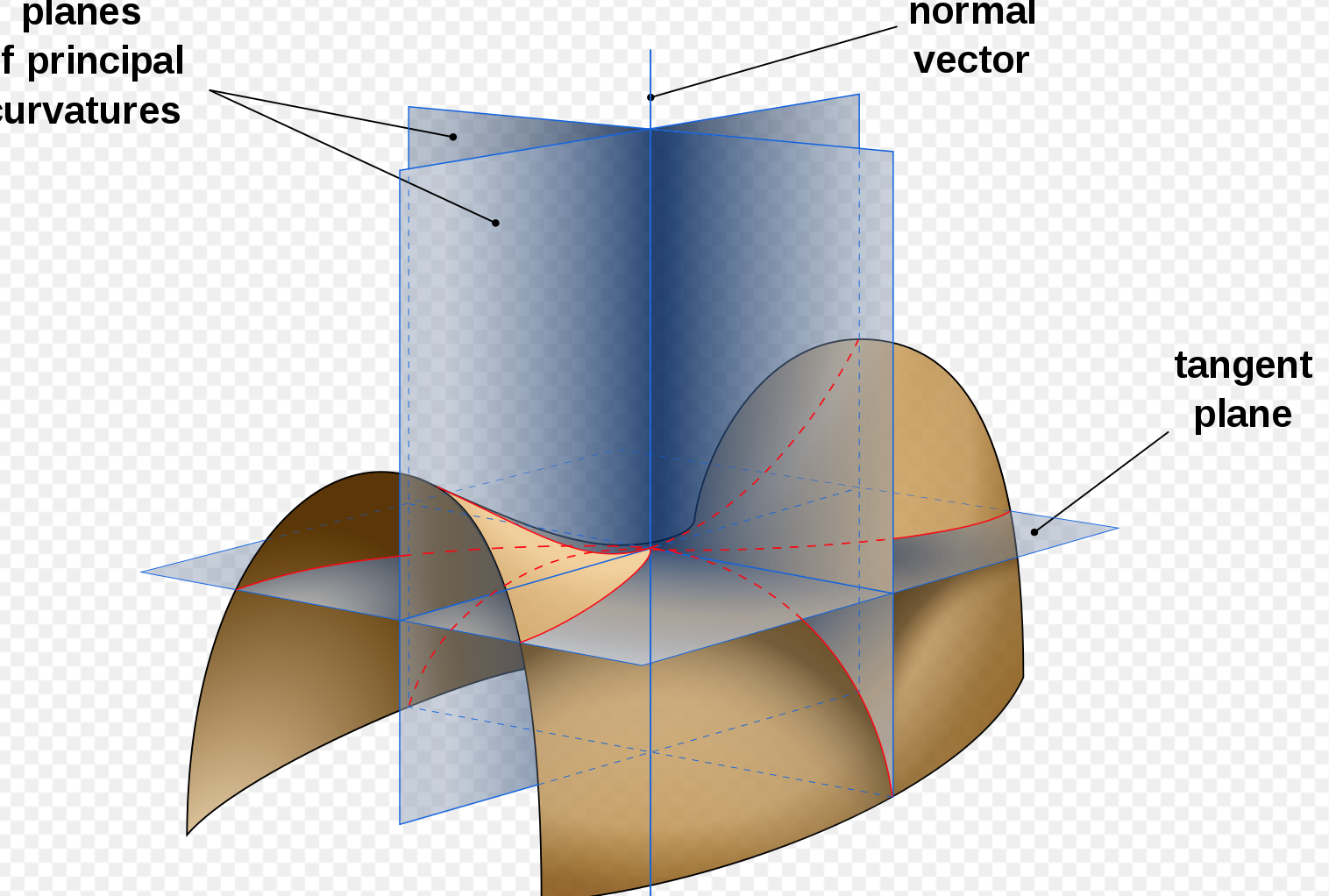
对于嵌入在欧几里得空间R3中的二维曲面,有两种曲率存在:高斯曲率和平均曲率。曲面上任意一点的法向量与某一 “切向量”所确定的平面的交集,这个交集是一个平面曲线

平均曲率显示曲面弯曲程度而高斯曲率无法表示可展开平面的弯曲程度如圆柱体
第二基本形式刻画了曲面离开切平面的弯曲程度,即 刻画了曲面在空间中的弯曲性
微分几何基础
第一基本形式,曲面的切空间中的内积,由$R^3$
第二基本形式,三维欧几里得空间中一个光滑曲面的切从上一个二次形式,记作II
平均曲率表示为$H={\frac {LG-2MF+NE}{2(EG-F^{2})}}$
DiffGeom2.2 和 DIffGeom 2.3 两篇文章对于如何求第一基本形式和第二基本形式做了数学上的推导
三角形网格离散化
这篇文章基于normal的计算三角形网格曲面曲率,方法有待验证
Discrete Differential-Geometry Operators for Triangulated 2-Manifolds) 这篇文章提出了Discrete Mean Curvature的估算方法
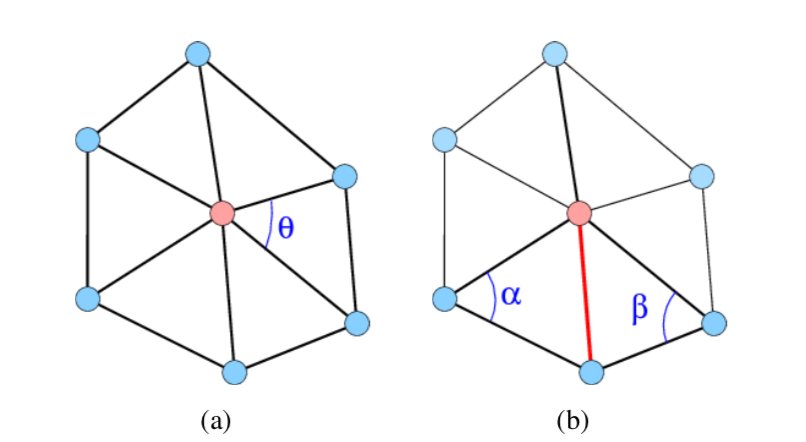
θ is the angle of one face at a vertex p used for computation of the discrete Gaussian curva- ture (a). α and β are the opposite angles to a given edge (here in red) used for computing the discrete mean curvature (b).
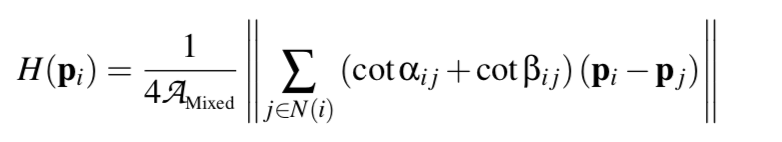
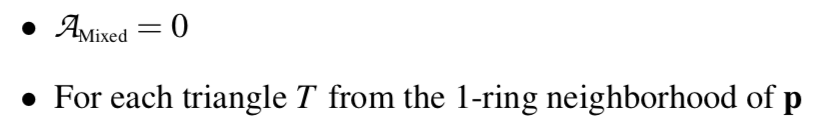
Estimating Curvatures and Their Derivatives on Triangle Meshes
这篇文章是对上面文章算法的改进
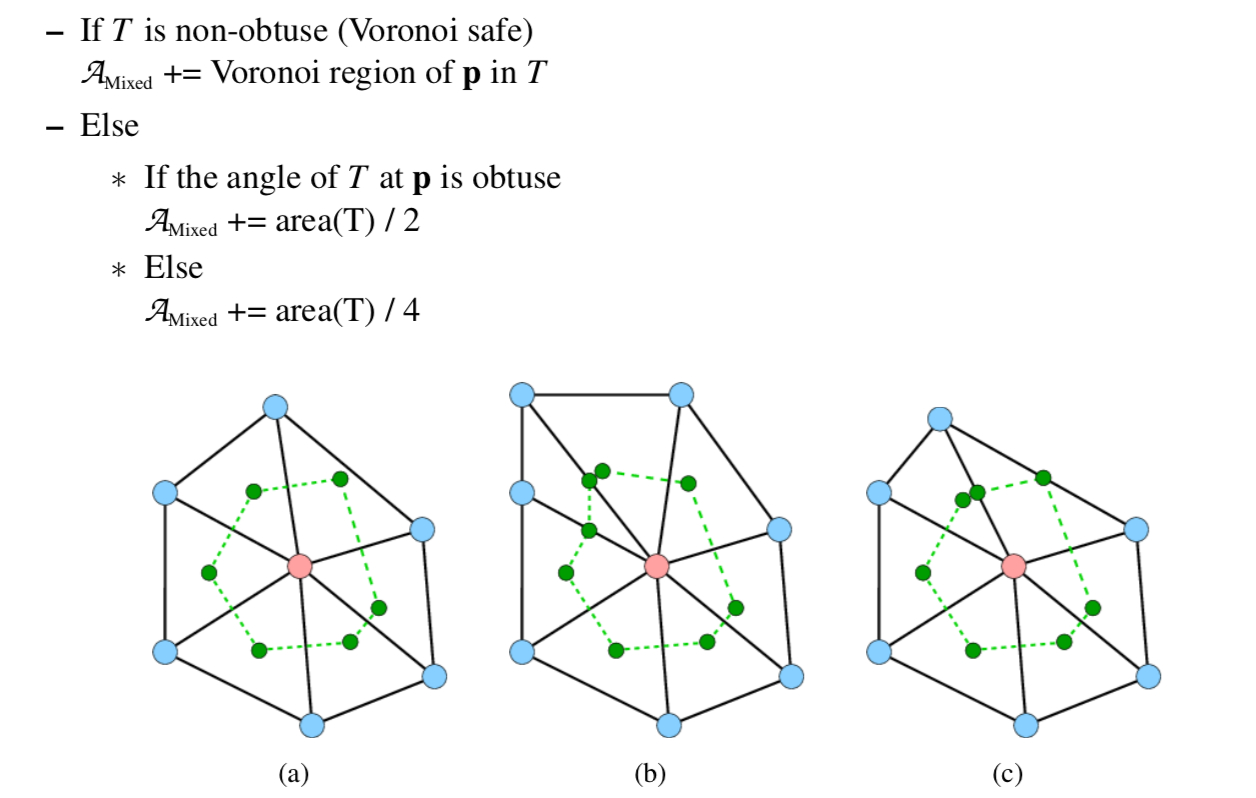
Algorithm :

这篇文章也用到了 Voronoi area 来做周边三角形面片的weighting
Reference link:
https://computergraphics.stackovernet.com/cn/q/251
https://zh.wikipedia.org/wiki/%E5%B9%B3%E5%9D%87%E6%9B%B2%E7%8E%87
https://zh.wikipedia.org/wiki/%E7%AC%AC%E4%BA%8C%E5%9F%BA%E6%9C%AC%E5%BD%A2%E5%BC%8F
https://blog.csdn.net/Jurbo/article/details/75046766
https://zh.wikipedia.org/wiki/%E4%B8%BB%E6%9B%B2%E7%8E%87
https://zh.wikipedia.org/wiki/%E8%B6%85%E5%B9%B3%E9%9D%A2
https://gfx.cs.princeton.edu/pubs/_2004_ECA/curvpaper.pdf